Get solution
11–2C By what properties is an electromagnetic wave characterized? How are these properties related to each other
Get solution
11–3C What is visible light? How does it differ from the other forms of electromagnetic radiation
Get solution
11–4C How do ultraviolet and infrared radiation differ? Do you think your body emits any radiation in the ultraviolet range? Explain
Get solution
11–5C What is thermal radiation? How does it differ from the other forms of electromagnetic radiation?
Get solution
11–6C What is the cause of color? Why do some objects appear blue to the eye while others appear red? Is the color of a surface at room temperature related to the radiation it emits
Get solution
11–7C Why is radiation usually treated as a surface phenomenon
Get solution
11–8C Why do skiers get sunburned so easily
Get solution
11–9C How does microwave cooking differ from conventional cooking
Get solution
11–10 Electricity is generated and transmitted in power lines at a frequency of 60 Hz (1 Hz 1 cycle per second). Determine the wavelength of the electromagnetic waves generated by the passage of electricity in power lines
Get solution
11–11 A microwave oven is designed to operate at a frequency of 2.8 x 109 Hz. Determine the wavelength of these microwaves and the energy of each microwave
Get solution
11–12 Aradio station is broadcasting radio waves at a wavelength of 200 m. Determine the frequency of these waves.
Get solution
11–13 A cordless telephone is designed to operate at a frequency of 8.5 x 108 Hz. Determine the wavelength of these telephone waves.
Get solution
11–14C What is a blackbody? Does a blackbody actually exist
Get solution
11–15C Define the total and spectral blackbody emissive powers. How are they related to each other? How do they differ
Get solution
11–16C Why did we define the blackbody radiation function? What does it represent? For what is it used
Get solution
11–17C Consider two identical bodies, one at 1000 K and the other at 1500 K. Which body emits more radiation in the shorter-wavelength region? Which body emits more radiation at a wavelength of 20 um
Get solution
11–18 Consider a 20-cm x 20-cm x 20-cm cubical body at 1000 K suspended in the air. Assuming the body closely approximates a blackbody, determine (a) the rate at which the cube emits radiation energy, in W, and (b) the spectral blackbody emissive power at a wavelength of 4 um
Get solution
11–19E The sun can be treated as a blackbody at an effective surface temperature of 10,400 R. Determine the rate at which infrared radiation energy (l=0.76–100 um) is emitted by the sun, in Btu/h · ft2
Get solution
11–20 The sun can be treated as a blackbody at 5780 K. Using EES (or other) software, calculate and plot the spectral blackbody emissive power Ebl of the sun versus wavelength in the range of 0.01 um to 1000 um. Discuss the results
Get solution
11–21 The temperature of the filament of an incandescent lightbulb is 3200 K. Treating the filament as a blackbody, determine the fraction of the radiant energy emitted by the filament that falls in the visible range. Also, determine the wavelength at which the emission of radiation from the filament peaks
Get solution
11–22 Reconsider Problem 11–21. Using EES (or other) software, investigate the effect of temperature on the fraction of radiation emitted in the visible range. Let the surface temperature vary from 1000 K to 4000 K, and plot fraction of radiation emitted in the visible range versus the surface temperature
Get solution
11–23 An incandescent lightbulb is desired to emit at least 15 percent of its energy at wavelengths shorter than 1 um. Determine the minimum temperature to which the filament of the lightbulb must be heated
Get solution
11–24 It is desired that the radiation energy emitted by a light source reach a maximum in the blue range (l=0.47 um). Determine the temperature of this light source and the fraction of radiation it emits in the visible range (l=0.40–0.76 um)
Get solution
11–25 A 3-mm-thick glass window transmits 90 percent of the radiation between l=0.3 and 3.0 um and is essentially opaque for radiation at other wavelengths. Determine the rate of radiation transmitted through a 2-m x 2-m glass window from blackbody sources at (a) 5800 K and (b) 1000 K.
Get solution
11–26C What does a solid angle represent, and how does it differ from a plane angle? What is the value of a solid angle associated with a sphere
Get solution
11–27C How is the intensity of emitted radiation defined? For a diffusely emitting surface, how is the emissive power related to the intensity of emitted radiation
Get solution
11–28C For a surface, how is irradiation defined? For diffusely incident radiation, how is irradiation on a surface related to the intensity of incident radiation
Get solution
11–29C For a surface, how is radiosity defined? For diffusely emitting and reflecting surfaces, how is radiosity related to the intensities of emitted and reflected radiation
Get solution
11–30C When the variation of spectral radiation quantity with wavelength is known, how is the corresponding total quantity determined?
Get solution
11–31 Asmall surface of area A1 =4 cm2 emits radiation as a blackbody at T1 = 800 K. Part of the radiation emitted by A1 strikes another small surface of area A2 = 4 cm2 oriented as shown in the figure. Determine the solid angle subtended by A2 when viewed from A1, and the rate at which radiation emitted by A1 that strikes A2 directly. What would your answer be if A2 were directly above A1 at a distance of 80 cm? Asmall circular surface of area A1 = 2 cm2 located at the center of a 2-m-diameter sphere emits radiation as a blackbody at T1 = 1000 K. Determine the rate at which radiation energy is streaming through a D2 = 1-cm-diameter hole located (a) on top of the sphere directly above A1 and (b) on the side of sphere such that the line that connects the centers of A1 and A2 makes 45˚ with surface A1.
Get solution
11–32 Asmall circular surface of area A1 2 cm2 located at the center of a 2-m-diameter sphere emits radiation as a blackbody at T1 1000 K. Determine the rate at which radiation energy is streaming through a D2 1-cm-diameter hole located (a) on top of the sphere directly above A1 and (b) on the side of sphere such that the line that connects the centers of A1 and A2 makes 45˚ with surface A1.
Get solution
11–33 Repeat Problem 11–32 for a 4-m-diameter sphere
Get solution
11–34 Asmall surface of area A = 1 cm2 emits radiation as a blackbody at 1500 K. Determine the rate at which radiation energy is emitted through a band defined by 0 ≤ O ≤ 2pi and 45 ≤ O ≤ 60˚ where is the angle a radiation beam makes with the normal of the surface and O is the azimuth angle
Get solution
11–35 Asmall surface of area A = 1 cm2 is subjected to incident radiation of constant intensity Ii = 2.2 x 104 W/m2 . sr over the entire hemisphere. Determine the rate at which radiation energy is incident on the surface through (a) 0 ≤ O ≤ 45˚ and (b) 45 ≤ O ≤ 90˚, where is the angle a radiation beam makes with the normal of the surface.
Get solution
11–36C Define the properties emissivity and absorptivity. When are these two properties equal to each other
Get solution
11–37C Define the properties reflectivity and transmissivity and discuss the different forms of reflection
Get solution
11–38C What is a graybody? How does it differ from a blackbody? What is a diffuse gray surface
Get solution
11–39C What is the greenhouse effect? Why is it a matter of great concern among atmospheric scientists
Get solution
11–40C We can see the inside of a microwave oven during operation through its glass door, which indicates that visible radiation is escaping the oven. Do you think that the harmful microwave radiation might also be escaping
Get solution
11–41 The spectral emissivity function of an opaque surface at 1000 K is approximated as
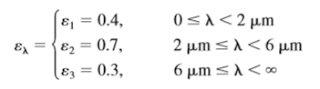
Determine the average emissivity of the surface and the rate of radiation emission from the surface, in W/m2.
Get solution
11–42 The reflectivity of aluminum coated with lead sulfate is 0.35 for radiation at wavelengths less than 3 um and 0.95 for radiation greater than 3 um. Determine the average reflectivity of this surface for solar radiation (T 5800 K) and radiation coming from surfaces at room temperature (T 300 K). Also, determine the emissivity and absorptivity of this surface at both temperatures. Do you think this material is suitable for use in solar collectors
Get solution
11–43 A furnace that has a 25-cm x 25-cm glass window can be considered to be a blackbody at 1200 K. If the transmissivity of the glass is 0.7 for radiation at wavelengths less than 3 um and zero for radiation at wavelengths greater than 3 um, determine the fraction and the rate of radiation coming from the furnace and transmitted through the window
Get solution
11–44 The emissivity of a tungsten filament can be approximated to be 0.5 for radiation at wavelengths less than 1 um and 0.15 for radiation at greater than 1 um. Determine the average emissivity of the filament at (a) 2000 K and (b) 3000 K. Also determine the absorptivity and reflectivity of the filament at both temperatures
Get solution
11–45 The variations of the spectral emissivity of two surfaces are as given in Figure P11–45. Determine the average emissivity of each surface at T 3000 K. Also, determine the average absorptivity and reflectivity of each surface for radiation coming from a source at 3000 K. Which surface is more suitable to serve as a solar absorber?
Get solution
11–46 The emissivity of a surface coated with aluminum oxide can be approximated to be 0.2 for radiation at wavelengths less than 5 um and 0.9 for radiation at wavelengths greater than 5 um. Determine the average emissivity of this surface at (a) 5800 K and (b) 300 K. What can you say about the absorptivity of this surface for radiation coming from sources at 5800 K and 300 K?
Get solution
11–47 The variation of the spectral absorptivity of a surface is as given in Figure P11–47. Determine the average absorptivity and reflectivity of the surface for radiation that originates from a source at T 2500 K. Also, determine the average emissivity of this surface at 3000 K.
Get solution
11–48E A5-in.-diameter spherical ball is known to emit radiation at a rate of 120 Btu/h when its surface temperature is 950 R. Determine the average emissivity of the ball at this temperature
Get solution
11–49 The variation of the spectral transmissivity of a 0.6-cm-thick glass window is as given in Figure P11–49. Determine the average transmissivity of this window for solar radiation (T 5800 K) and radiation coming from surfaces at room temperature (T 300 K). Also, determine the amount of solar radiation transmitted through the window for incident solar radiation of 650 W/m2.
Get solution
11–50C What is the solar constant? How is it used to determine the effective surface temperature of the sun? How would the value of the solar constant change if the distance between the earth and the sun doubled
Get solution
11–51C What changes would you notice if the sun emitted radiation at an effective temperature of 2000 K instead of 5762 K
Get solution
11–52C Explain why the sky is blue and the sunset is yelloworange
Get solution
11–53C When the earth is closest to the sun, we have winter in the northern hemisphere. Explain why. Also explain why we have summer in the northern hemisphere when the earth is farthest away from the sun
Get solution
11–54C What is the effective sky temperature
Get solution
11–55C You have probably noticed warning signs on the highways stating that bridges may be icy even when the roads are not. Explain how this can happen
Get solution
11–56C Unless you live in a warm southern state, you have probably had to scrape ice from the windshield and windows of your car many mornings. You may have noticed, with frustration, that the thickest layer of ice always forms on the windshield instead of the side windows. Explain why this is the case
Get solution
11–57C Explain why surfaces usually have quite different absorptivities for solar radiation and for radiation originating from the surrounding bodies
Get solution
11–58 A surface has an absorptivity of as = 0.85 for solar radiation and an emissivity of E=0.5 at room temperature. The surface temperature is observed to be 350 K when the direct and the diffuse components of solar radiation are GD = 350 and Gd = 400 W/m2, respectively, and the direct radiation makes a 30° angle with the normal of the surface. Taking the effective sky temperature to be 280 K, determine the net rate of radiation heat transfer to the surface at that time.
Get solution
11–59E Solar radiation is incident on the outer surface of a spaceship at a rate of 400 Btu/h · ft2. The surface has an absorptivity of as = 0.10 for solar radiation and an emissivity of E=0.8 at room temperature. The outer surface radiates heat into space at 0 R. If there is no net heat transfer into the spaceship, determine the equilibrium temperature of the surface. The air temperature on a clear night is observed to remain at about 4°C. Yet water is reported to have frozen that night due to radiation effect. Taking the convection heat transfer coefficient to be 18 W/m2 · °C, determine the value of the maximum effective sky temperature that night.
Get solution
11–60 The air temperature on a clear night is observed to remain at about 4°C. Yet water is reported to have frozen that night due to radiation effect. Taking the convection heat transfer coefficient to be 18 W/m2 · °C, determine the value of the maximum effective sky temperature that night
Get solution
11–61 The absorber surface of a solar collector is made of aluminum coated with black chrome (as = 0.87 and E=0.09). Solar radiation is incident on the surface at a rate of 600 W/m2. The air and the effective sky temperatures are 25°C and 15°C, respectively, and the convection heat transfer coefficient is 10 W/m2 · °C. For an absorber surface temperature of 70°C, determine the net rate of solar energy delivered by the absorber plate to the water circulating behind it.
Get solution
11–62 Reconsider Problem 11–61. Using EES (or other) software, plot the net rate of solar energy transferred to water as a function of the absorptivity of the absorber plate. Let the absorptivity vary from 0.5 to 1.0, and discuss the results
Get solution
11–63 Determine the equilibrium temperature of the absorber surface in Problem 11–61 if the back side of the absorber is insulated.
Get solution
11–64C What fraction of the solar energy is in the visible range (a) outside the earth’s atmosphere and (b) at sea level on earth? Answer the same question for infrared radiation
Get solution
11–65C Describe the solar radiation properties of a window that is ideally suited for minimizing the air-conditioning load.
Get solution
11–66C Define the SHGC (solar heat gain coefficient), and explain how it differs from the SC (shading coefficient). What are the values of the SHGC and SC of a single-pane clear-glass window
Get solution
11–67C What does the SC (shading coefficient) of a device represent? How do the SCs of clear glass and heat-absorbing glass compare
Get solution
11–68C What is a shading device? Is an internal or external shading device more effective in reducing the solar heat gain through a window? How does the color of the surface of a shading device facing outside affect the solar heat gain
Get solution
11–69C What is the effect of a low-e coating on the inner surface of a window glass on the (a) heat loss in winter and (b) heat gain in summer through the window
Get solution
11–70C What is the effect of a reflective coating on the outer surface of a window glass on the (a) heat loss in winter and (b) heat gain in summer through the window
Get solution
11–71 Amanufacturing facility located at 32° N latitude has a glazing area of 60 m2 facing west that consists of doublepane windows made of clear glass (SHGC 0.766). To reduce the solar heat gain in summer, a reflective film that will reduce the SHGC to 0.35 is considered. The cooling season consists of June, July, August, and September, and the heating season, October through April. The average daily solar heat fluxes incident on the west side at this latitude are 2.35, 3.03, 3.62, 4.00, 4.20, 4.24, 4.16, 3.93, 3.48, 2.94, 2.33, and 2.07 kWh/day · m2 for January through December, respectively. Also, the unit costs of electricity and natural gas are $0.09/kWh and $0.45/therm, respectively. If the coefficient of performance of the cooling system is 3.2 and the efficiency of the furnace is 0.90, determine the net annual cost savings due to installing reflective coating on the windows. Also, determine the simple payback period if the installation cost of reflective film is $20/m2.
Get solution
11–72 Ahouse located in Boulder, Colorado (40°N latitude), has ordinary double-pane windows with 6-mm-thick glasses and the total window areas are 8, 6, 6, and 4 m2 on the south, west, east, and north walls, respectively. Determine the total solar heat gain of the house at 9:00, 12:00, and 15:00 solar time in July. Also, determine the total amount of solar heat gain per day for an average day in January
Get solution
11–73 Repeat Problem 11–72 for double-pane windows that are gray-tinted
Get solution
11–74 Consider a building in New York (40° N latitude) that has 200 m2 of window area on its south wall. The windows are double-pane heat-absorbing type, and are equipped with lightcolored venetian blinds with a shading coefficient of SC 0.30. Determine the total solar heat gain of the building through the south windows at solar noon in April. What would your answer be if there were no blinds at the windows?
Get solution
11–75 Atypical winter day in Reno, Nevada (39°N latitude), is cold but sunny, and thus the solar heat gain through the windows can be more than the heat loss through them during daytime. Consider a house with double-door-type windows that are double paned with 3-mm-thick glasses and 6.4 mm of air space and have aluminum frames and spacers. The house is maintained at 22°C at all times. Determine if the house is losing more or less heat than it is gaining from the sun through an east window on a typical day in January for a 24-h period if the average outdoor temperature is 10°C.
Get solution
11–76 Repeat Problem 11–75 for a south window
Get solution
11–77E Determine the rate of net heat gain (or loss) through a 9-ft-high, 15-ft-wide, fixed -in. single-glass window with aluminum frames on the west wall at 3 PM solar time during a typical day in January at a location near 40° N latitude when the indoor and outdoor temperatures are 70°F and 45°F, respectively.
Get solution
11–78 Consider a building located near 40° N latitude that has equal window areas on all four sides. The building owner is considering coating the south-facing windows with reflective film to reduce the solar heat gain and thus the cooling load. But someone suggests that the owner will reduce the cooling load even more if she coats the west-facing windows instead. What do you think?
Get solution
11–79 The spectral emissivity of an opaque surface at 1200 K is approximated as

Determine the total emissivity and the emissive flux of the surface
Get solution
11–80 The spectral transmissivity of a 3-mm-thick regular glass can be expressed as

Determine the transmissivity of this glass for solar radiation. What is the transmissivity of this glass for light
Get solution
11–81 A 1-m-diameter spherical cavity is maintained at a uniform temperature of 600 K. Now a 5-mm-diameter hole is drilled. Determine the maximum rate of radiation energy streaming through the hole. What would your answer be if the diameter of the cavity were 3 m
Get solution
11–82 The spectral absorptivity of an opaque surface is as shown on the graph. Determine the absorptivity of the surface for radiation emitted by a source at (a) 1000 K and (b) 3000 K.
Get solution
11–83 The surface in Problem 11–82 receives solar radiation at a rate of 820 W/m2. Determine the solar absorptivity of the surface and the rate of absorption of solar radiation
Get solution
11–84 The spectral transmissivity of a glass cover used in a solar collector is given as

Solar radiation is incident at a rate of 950 W/m2, and the absorber plate, which can be considered to be black, is maintained at 340 K by the cooling water. Determine (a) the solar flux incident on the absorber plate, (b) the transmissivity of the glass cover for radiation emitted by the absorber plate, and (c) the rate of heat transfer to the cooling water if the glass cover temperature is also 340 K
Get solution
11–85 Consider a small black surface of area A = 2 cm2 maintained at 600 K. Determine the rate at which radiation energy is emitted by the surface through a ring-shaped opening defined by 0 ≤ O ≤ 2pi and 40 ≤ O ≤ 50˚ where O is the azimuth angle and is the angle a radiation beam makes with the normal of the surface.
Get solution