Get solution
15–2C What is an integrated circuit? What is its significance in the electronics era? What do the initials MSI, LSI, and VLSI stand for?
Get solution
15–3C When electric current I passes through an electrical element having a resistance R, why is heat generated in the element? How is the amount of heat generation determined
Get solution
15–4C Consider a TV that is wrapped in the blankets from all sides except its screen. Explain what will happen when the TV is turned on and kept on for a long time, and why. What will happen if the TV is kept on for a few minutes only
Get solution
15–5C Consider an incandescent light bulb that is completely wrapped in a towel. Explain what will happen when the light is turned on and kept on. (P.S. Do not try this at home!)
Get solution
15–6C A businessman ties a large cloth advertisement banner in front of his car such that it completely blocks the airflow to the radiator. What do you think will happen when he starts the car and goes on a trip?
Get solution
15–7C Which is more likely to break: a car or a TV? Why
Get solution
15–8C Why do electronic components fail under prolonged use at high temperatures
Get solution
15–9 The temperature of the case of a power transistor that is dissipating 12 W is measured to be 60°C. If the junction-tocase thermal resistance of this transistor is specified by the manufacturer to be 5°C/W, determine the junction temperature of the transistor.
Get solution
15–10 Power is supplied to an electronic component from a 12-V source, and the variation in the electric current, the junction temperature, and the case temperatures with time are observed. When everything is stabilized, the current is observed to be 0.15 Aand the temperatures to be 80°C and 55°C at the junction and the case, respectively. Calculate the junction-tocase thermal resistance of this component
Get solution
15–11 A logic chip used in a computer dissipates 6 W of power in an environment at 55°C and has a heat transfer surface area of 0.32 cm2. Assuming the heat transfer from the surface to be uniform, determine (a) the amount of heat this chip dissipates during an 8-h work day, in kWh, and (b) the heat flux on the surface of the chip, in W/cm2
Get solution
15–12 A 15 –cm x 20-cm circuit board houses 90 closely spaced logic chips, each dissipating 0.1 W, on its surface. If the heat transfer from the back surface of the board is negligible, determine (a) the amount of heat this circuit board dissipates during a 10-h period, in kWh, and (b) the heat flux on the surface of the circuit board, in W/cm2.
Get solution
15–13E A resistor on a circuit board has a total thermal resistance of 130°F/W. If the temperature of the resistor is not to exceed 360°F, determine the power at which it can operate safely in an ambient at 120°F
Get solution
15–14 Consider a 0.1-kΩ resistor whose surface-to-ambient thermal resistance is 300°C/W. If the voltage drop across the resistor is 7.5 V and its surface temperature is not to exceed 150°C, determine the power at which it can operate safely in an ambient at 30°C.
Get solution
15–15 Reconsider Problem 15–14. Using EES (or other) software, plot the power at which the resistor can operate safely as a function of the ambient temperature as the temperature varies from 20ºC to 40ºC, and discuss the results.
Get solution
15–16C Why is a chip in a chip carrier bonded to a lead frame instead of the plastic case of the chip carrier
Get solution
15–17C Draw a schematic of a chip carrier, and explain how heat is transferred from the chip to the medium outside of the chip carrier
Get solution
15–18C What does the junction-to-case thermal resistance represent? On what does it depend for a chip carrier
Get solution
15–19C What is a hybrid chip carrier? What are the advantages of hybrid electronic packages
Get solution
15–20C What is a PCB? Of what is the board of a PCB made? What does the “device-to-PCB edge” thermal resistance in conduction-cooled systems represent? Why is this resistance relatively high
Get solution
15–21C What are the three types of printed circuit boards? What are the advantages and disadvantages of each type
Get solution
15–22C What are the desirable characteristics of the materials used in the fabrication of the circuit boards
Get solution
15–23C What is an electronic enclosure? What is the primary function of the enclosure of an electronic system? Of what materials are the enclosures made?
Get solution
15–24C Consider an electronics box that consumes 120 Wof power when plugged in. How is the heating load of this box determined
Get solution
15–25C Why is the development of superconducting materials generating so much excitement among designers of electronic equipment
Get solution
15–26C How is the duty cycle of an electronic system defined? How does the duty cycle affect the design and selection of a cooling technique for a system
Get solution
15–27C What is temperature cycling? How does it affect the reliability of electronic equipment
Get solution
15–28C What is the ultimate heat sink for (a) a TV, (b) an airplane, and (c) a ship? For each case, what is the range of temperature variation of the ambient
Get solution
15–29C What is the ultimate heat sink for (a) a VCR, (b) a spacecraft, and (c) a communication system on top of a mountain? For each case, what is the range of temperature variation of the ambient?
Get solution
15–30C How are the electronics of short-range and longrange missiles cooled
Get solution
15–31C What is dynamic temperature? What causes it? How is it determined? At what velocities is it significant
Get solution
15–32C How are the electronics of a ship or submarine cooled
Get solution
15–33C How are the electronics of the communication systems at remote areas cooled
Get solution
15–34C How are the electronics of high-power microwave equipment such as radars cooled
Get solution
15–35C How are the electronics of a space vehicle cooled
Get solution
15–36 Consider an airplane cruising in the air at a temperature of -25°C at a velocity of 850 km/h. Determine the temperature rise of air at the nose of the airplane as a result of the ramming effect of the air.
Get solution
15–37 The temperature of air in high winds is measured by a thermometer to be 12°C. Determine the true temperature of air if the wind velocity is 90 km/h.
Get solution
15–38 Reconsider Problem 15–37. Using EES (or other) software, plot the true temperature of air as a function of the wind velocity as the velocity varies from 20 km/h to 120 km/h, and discuss the results
Get solution
15–39 Air at 25°C is flowing in a channel at a velocity of (a) 1, (b) 10, (c) 100, and (d) 1000 m/s. Determine the temperature that a stationary probe inserted into the channel will read for each case
Get solution
15–40 An electronic device dissipates 2 W of power and has a surface area of 5 cm2. If the surface temperature of the device is not to exceed the ambient temperature by more than 50°C, determine a suitable cooling technique for this device. Use Figure 15–17
Get solution
15–41E Astand-alone circuit board, 6 in. x 8 in. in size, dissipates 20 Wof power. The surface temperature of the board is not to exceed 165°F in an 85°F environment. Using Figure 15–17 as a guide, select a suitable cooling mechanism.
Get solution
15–42C What are the major considerations in the selection of a cooling technique for electronic equipment
Get solution
15–43C What is thermal resistance? To what is it analogous in electrical circuits? Can thermal resistance networks be analyzed like electrical circuits? Explain
Get solution
15–44C If the rate of heat conduction through a medium and the thermal resistance of the medium are known, how can the temperature difference between the two sides of the medium be determined
Get solution
15–45C Consider a wire of electrical resistance R, length L, and cross-sectional area A through which electric current I is flowing. How is the voltage drop across the wire determined? What happens to the voltage drop when L is doubled while I is held constant? Now consider heat conduction at a rate of Q · through the same wire having a thermal resistance of R. How is the temperature drop across the wire determined? What happens to the temperature drop when L is doubled while Q · is held constant?
Get solution
15–46C What is a heat frame? How does it enhance heat transfer along a PCB? Which components on a PCB attached to a heat frame operate at the highest temperatures: those at the middle of the PCB or those near the edge
Get solution
15–47C What is constriction resistance in heat flow? To what is it analogous in fluid flow through tubes and electric current flow in wires
Get solution
15–48C What does the junction-to-case thermal resistance of an electronic component represent? In practice, how is this value determined? How can the junction temperature of a component be determined when the case temperature, the power dissipation of the component, and the junction-to-case thermal resistance are known
Get solution
15–49C What does the case-to-ambient thermal resistance of an electronic component represent? In practice, how is this value determined? How can the case temperature of a component be determined when the ambient temperature, the power dissipation of the component, and the case-to-ambient thermal resistance are known
Get solution
15–50C Consider an electronic component whose junction-tocase thermal resistance Rjunction-case is provided by the manufacturer and whose case-to-ambient thermal resistance Rcase-ambient is determined by the thermal designer. When the power dissipation of the component and the ambient temperature are known, explain how the junction temperature can be determined. When Rjunction-case is greater than Rcase-ambient, will the case temperature be closer to the junction or ambient temperature
Get solution
15–51C Why is the rate of heat conduction along a PCB very low? How can heat conduction from the mid-parts of a PCB to its outer edges be improved? How can heat conduction across the thickness of the PCB be improved
Get solution
15–52C Why is the warping of epoxy boards that are coppercladded on one side a major concern? What is the cause of this warping? How can the warping of PCBs be avoided
Get solution
15–53C Why did the thermal conduction module receive so much attention from thermal designers of electronic equipment? How does the design of TCM differ from traditional chip carrier design? Why is the cavity in the TCM filled with helium instead of air
Get solution
15–54 Consider a chip dissipating 0.8 W of power in a DIP with 18 pin leads. The materials and the dimensions of various sections of this electronic device are given in the table.
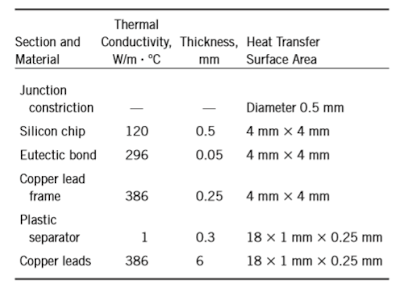
If the temperature of the leads is 50°C, estimate the temperature at the junction of the chip.
Get solution
15–55 A fan blows air at 25°C over a 2-W plastic DIP with 16 leads mounted on a PCB at a velocity of 300 m/min. Using data from Figure 15–23, determine the junction temperature of the electronic device. What would the junction temperature be if the fan were to fail
Get solution
15–56 Heat is to be conducted along a PCB with copper cladding on one side. The PCB is 12 cm long and 12 cm wide, and the thicknesses of the copper and epoxy layers are 0.06 mm and 0.5 mm, respectively. Disregarding heat transfer from the side surfaces, determine the percentages of heat conduction along the copper (k 386 W/m · °C) and epoxy (k 0.26 W/m · °C) layers. Also, determine the effective thermal conductivity of the PCB.
Get solution
15–57 Reconsider Problem 15–56. Using EES (or other) software, investigate the effect of the thickness of the copper layer on the percentage of heat conducted along the copper layer and the effective thermal conductivity of the PCB. Let the thickness vary from 0.02 mm to 0.10 mm. Plot the percentage of heat conducted along the copper layer and the effective thermal conductivity as a function of the thickness of the copper layer, and discuss the results
Get solution
15–58 The heat generated in the circuitry on the surface of a silicon chip (k 130 W/m · °C) is conducted to the ceramic substrate to which it is attached. The chip is 6 mm 6 mm in size and 0.5-mm thick and dissipates 3Wof power. Determine the temperature difference between the front and back surfaces of the chip in steady operation
Get solution
15–59E Consider a 6-in. 7-in. glass–epoxy laminate (k 0.15 Btu/h · ft ·°F) whose thickness is 0.05 in. Determine the thermal resistance of this epoxy layer for heat flow (a) along the 7-in.-long side and (b) across its thickness
Get solution
15–60 Consider a 15–cm x 18-cm glass–epoxy laminate (k 0.26 W/m ·°C) whose thickness is 1.4 mm. In order to reduce the thermal resistance across its thickness, cylindrical copper fillings (k 386 W/m · °C) of diameter 1 mm are to be planted throughout the board with a center-to-center distance of 3 mm. Determine the new value of the thermal resistance of the epoxy board for heat conduction across its thickness as a result of this modification
Get solution
15–61 Reconsider Problem 15–60. Using EES (or other) software, investigate the effects of the thermal conductivity and the diameter of the filling material on the thermal resistance of the epoxy board. Let the thermal conductivity vary from 10 W/m · 0C to 400 W/m · 0C and the diameter from 0.5 mm to 2.0 mm. Plot the thermal resistance as functions of the thermal conductivity and the diameter, and discuss the results
Get solution
15–62 A 12-cm 15–cm circuit board dissipating 45 W of heat is to be conduction-cooled by a 1.5-mm-thick copper heat frame (k 386 W/m · °C) 12 cm x 17 cm in size. The epoxy laminate (k 0.26 W/m · °C) has a thickness of 2 mm and is attached to the heat frame with conductive epoxy adhesive (k 1.8 W/m · °C) of thickness 0.12 mm. The PCB is attached to a heat sink by clamping a 5-mm-wide portion of the edge to the heat sink from both ends. The temperature of the heat frame at this point is 30°C. Heat is uniformly generated on the PCB at a rate of 3 Wper 1-cm x 12-cm strip. Considering only onehalf of the PCB board because of symmetry, determine the maximum surface temperature on the PCB and the temperature distribution along the heat frame.
Get solution
15–63 Consider a 15–cm x 20-cm double-sided circuit board dissipating a total of 30 Wof heat. The board consists of a 3-mm-thick epoxy layer (k 0.26 W/m · °C) with 1-mm-diameter aluminum wires (k 237 W/m · °C) inserted along the 20-cm-long direction, as shown in Figure P15–63. The distance between the centers of the aluminum wires is 2 mm. The circuit board is attached to a heat sink from both ends, and the temperature of the board at both ends is 30°C. Heat is considered to be uniformly generated on both sides of the epoxy layer of the PCB. Considering only a portion of the PCB because of symmetry, determine the magnitude and location of the maximum temperature that occurs in the PCB.
Get solution
15–64 Repeat Problem 15–63, replacing the aluminum wires by copper wires (k 386 W/m · °C)
Get solution
15–65 Repeat Problem 15–63 for a center-to-center distance of 4 mm instead of 2 mm between the wires
Get solution
15–66 Consider a thermal conduction module with 80 chips, each dissipating 4 W of power. The module is cooled by water at 18°C flowing through the cold plate on top of the module. The thermal resistances in the path of heat flow are Rchip 12°C/W between the junction and the surface of the chip, Rint 9°C/W between the surface of the chip and the outer surface of the thermal conduction module, and Rext 7°C/W between the outer surface of the module and the cooling water. Determine the junction temperature of the chip
Get solution
15–67 Consider a 0.3-mm-thick epoxy board (k 0.26 W/m · °C) that is 15 cm 20 cm in size. Now a 0.1-mm-thick layer of copper (k 386 W/m ·°C) is attached to the back surface of the PCB. Determine the effective thermal conductivity of the PCB along its 20-cm-long side. What fraction of the heat conducted along that side is conducted through copper
Get solution
15–68 A 0.5-mm-thick copper plate (k 386 W/m · °C) is sandwiched between two 3-mm-thick epoxy boards (k 0.26 W/m · °C) that are 12 cm x 18 cm in size. Determine the effective thermal conductivity of the PCB along its 18-cm-long side. What fraction of the heat conducted along that side is conducted through copper?
Get solution
15–69E A 6-in. x 8-in. x 0.06-in. copper heat frame is used to conduct 20 W of heat generated in a PCB along the 8-in.-long side toward the ends. Determine the temperature difference between the midsection and either end of the heat frame.
Get solution
15–70 A12-W power transistor is cooled by mounting it on an aluminum bracket (k 237 W/m · °C) that is attached to a liquid-cooled plate by 0.2-mm-thick epoxy adhesive (k 1.8 W/m · °C), as shown in Figure P15–70. The thermal resistance of the plastic washer is given as 2.5°C/W. Preliminary calculations show that about 20 percent of the heat is dissipated by convection and radiation, and the rest is conducted to the liquid-cooled plate. If the temperature of the cold plate is 50°C, determine the temperature of the transistor case.
Get solution
15–71C A student puts his books on top of a VCR, completely blocking the air vents on the top surface. What do you think will happen as the student watches a rented movie played by that VCR
Get solution
15–72C Can a low-power electronic system in space be cooled by natural convection? Can it be cooled by radiation? Explain
Get solution
15–73C Why are there several openings on the various surfaces of a TV, VCR, and other electronic enclosures? What happens if a TV or VCR is enclosed in a cabinet with no free air space around
Get solution
15–74C Why should radiation heat transfer always be considered in the analysis of natural convection–cooled electronic equipment
Get solution
15–75C How does atmospheric pressure affect natural convection heat transfer? What are the best and worst orientations for heat transfer from a square surface
Get solution
15–76C What is view factor? How does it affect radiation heat transfer between two surfaces
Get solution
15–77C What is emissivity? How does it affect radiation heat transfer between two surfaces?
Get solution
15–78C For most effective natural convection cooling of a PCB array, should the PCBs be placed horizontally or vertically? Should they be placed close to each other or far from each other
Get solution
15–79C Why is radiation heat transfer from the components on the PCBs in an enclosure negligible
Get solution
15–80 Consider a sealed 20-cm-high electronic box whose base dimensions are 35 cm x 50 cm that is placed on top of a stand in a room at 30°C. The emissivity of the outer surface of the box is 0.85. If the electronic components in the box dissipate a total of 100 Wof power and the outer surface temperature of the box is not to exceed 65°C, determine if this box can be cooled by natural convection and radiation alone. Assume the heat transfer from the bottom surface of the box to the stand to be negligible, and the temperature of the surrounding surfaces to be the same as the air temperature of the room.
Get solution
15–81 Repeat Problem 15–80, assuming the box is mounted on a wall instead of a stand such that it is 0.5 m high. Again, assume heat transfer from the bottom surface to the wall to be negligible
Get solution
15–82E A 0.15-W small cylindrical resistor mounted on a circuit board is 0.5 in. long and has a diameter of 0.15 in. The view of the resistor is largely blocked by the circuit board facing it, and the heat transfer from the connecting wires is negligible. The air is free to flow through the parallel flow passages between the PCBs as a result of natural convection currents. If the air temperature in the vicinity of the resistor is 130°F, determine the surface temperature of the resistor.
Get solution
15–83 A14-cm x 20-cm PCB has electronic components on one side, dissipating a total of 7 W. The PCB is mounted in a rack vertically (height 14 cm) together with other PCBs. If the surface temperature of the components is not to exceed 90°C, determine the maximum temperature of the environment in which this PCB can operate safely at sea level. What would your answer be if this rack is located at a location at 3000 m altitude where the atmospheric pressure is 70.12 kPa?
Get solution
15–84 Acylindrical electronic component whose diameter is 2 cm and length is 4 cm is mounted on a board with its axis in the vertical direction and is dissipating 3 W of power. The emissivity of the surface of the component is 0.8, and the temperature of the ambient air is 30°C. Assuming the temperature of the surrounding surfaces to be 20°C, determine the average surface temperature of the component under combined natural convection and radiation cooling
Get solution
15–85 Repeat Problem 15–84, assuming the component is oriented horizontally
Get solution
15–86 Reconsider Problem 15–84. Using EES (or other) software, investigate the effects of surface emissivity and ambient temperature on the average surface temperature of the component. Let the emissivity vary from 0.1 to 1.0 and the ambient temperature from 15ºC to 35ºC. Take the temperature of the surrounding surfaces to be 10ºC smaller than the ambient air temperature. Plot the average surface temperature as functions of the emissivity and the ambient air temperature, and discuss the results
Get solution
15–87 Consider a power transistor that dissipates 0.1 W of power in an environment at 30°C. The transistor is 0.4 cm long and has a diameter of 0.4 cm. Assuming heat to be transferred uniformly from all surfaces, determine (a) the heat flux on the surface of the transistor, in W/cm2, and (b) the surface temperature of the transistor for a combined convection and radiation heat transfer coefficient of 18 W/m2 · °C
Get solution
15–88 The components of an electronic system dissipating 150 W are located in a 1-m-long horizontal duct whose cross section is 15 cm x 15 cm. The components in the duct are cooled by forced air, which enters at 30°C at a rate of 0.4 m3/min and leaves at 45°C. The surfaces of the sheet metal duct are not painted, and thus radiation heat transfer from the outer surfaces is negligible. If the ambient air temperature is 25°C, determine (a) the heat transfer from the outer surfaces of the duct to the ambient air by natural convection and (b) the average temperature of the duct.
Get solution
15–89 Repeat Problem 15–88 for a circular horizontal duct of diameter 10 cm
Get solution
15–90 Reconsider Problem 15–88. Using EES (or other) software, investigate the effects of the volume flow rate of air and the side-length of the duct on heat transfer by natural convection and the average temperature of the duct. Let the flow rate vary from 0.1 m3/min to 0.5 m3/min, and the side-length from 10 cm to 20 cm. Plot the heat transfer rate by natural convection and the average duct temperature as functions of flow rate and side-length, and discuss the results
Get solution
15–91 Repeat Problem 15–88, assuming that the fan fails and thus the entire heat generated inside the duct must be rejected to the ambient air by natural convection from the outer surfaces of the duct
Get solution
15–92 A 20-cm x 20-cm circuit board containing 81 square chips on one side is to be cooled by combined natural convection and radiation by mounting it on a vertical surface in a room at 25°C. Each chip dissipates 0.08 W of power, and the emissivity of the chip surfaces is 0.65. Assuming the heat transfer from the back side of the circuit board to be negligible and the temperature of the surrounding surfaces to be the same as the air temperature of the room, determine the surface temperature of the chips
Get solution
15–93 Repeat Problem 15–92, assuming the circuit board to be positioned horizontally with (a) chips facing up and (b) chips facing down.
Get solution
15–94C Why is radiation heat transfer in forced-air-cooled systems disregarded
Get solution
15–95C If an electronic system can be cooled adequately by either natural convection or forced-air convection, which would you prefer? Why
Get solution
15–96C Why is forced convection cooling much more effective than natural convection cooling
Get solution
15–97C Consider a forced-air-cooled electronic system dissipating a fixed amount of power. How will increasing the flow rate of air affect the surface temperature of the components? Explain. How will it affect the exit temperature of the air
Get solution
15–98C To what do internal and external flow refer in forced convection cooling? Give an example of a forced-air-cooled electronic system that involves both types of flow
Get solution
15–99C For a specified power dissipation and air inlet temperature, how does the convection heat transfer coefficient affect the surface temperature of the electronic components? Explain
Get solution
15–100C How does high altitude affect forced convection heat transfer? How would you modify your forced-air cooling system to operate at high altitudes safely
Get solution
15–101C What are the advantages and disadvantages of placing the cooling fan at the inlet or at the exit of an electronic box
Get solution
15–102C How is the volume flow rate of air in a forced-aircooled electronic system that has a constant-speed fan established? If a few more PCBs are added to the box while keeping the fan speed constant, will the flow rate of air through the system change? Explain
Get solution
15–103C What happens if we attempt to cool an electronic system with an undersized fan? What about if we do that with an oversized fan
Get solution
15–104 Consider a hollow-core PCB that is 15 cm high and 20 cm long, dissipating a total of 30 W. The width of the air gap in the middle of the PCB is 0.25 cm. The cooling air enters the core at 30°C at a rate of 1 L/s. Assuming the heat generated to be uniformly distributed over the two side surfaces of the PCB, determine (a) the temperature at which the air leaves the hollow core and (b) the highest temperature on the inner surface of the core.
Get solution
15–105 Repeat Problem 15–104 for a hollow-core PCB dissipating 45 W
Get solution
15–106 Reconsider Problem 15–104. Using EES (or other) software, investigate the effects of the power rating of the PCB and the volume flow rate of the air on the exit temperature of the air and the maximum temperature on the inner surface of the core. Let the power vary from 20 W to 60 W and the flow rate from 0.5 L/s to 2.5 L/s. Plot the air exit temperature and the maximum surface temperature of the core as functions of power and flow rate, and discuss the results
Get solution
15–107E Atransistor with a height of 0.25 in. and a diameter of 0.2 in. is mounted on a circuit board. The transistor is cooled by air flowing over it at a velocity of 400 ft/min. If the air temperature is 140°F and the transistor case temperature is not to exceed 175°F, determine the amount of power this transistor can dissipate safely.
Get solution
15–108 A desktop computer is to be cooled by a fan. The electronic components of the computer consume 75 W of power under full-load conditions. The computer is to operate in environments at temperatures up to 45°C and at elevations up to 3400 m where the atmospheric pressure is 66.63 kPa. The exit temperature of air is not to exceed 60°C to meet reliability requirements. Also, the average velocity of air is not to exceed 110 m/min at the exit of the computer case, where the fan is installed to keep the noise level down. Determine the flow rate of the fan that needs to be installed and the diameter of the casing of the fan
Get solution
15–109 Repeat Problem 15–108 for a computer that consumes 100 W of power
Get solution
15–110 A computer cooled by a fan contains eight PCBs, each dissipating 12 W of power. The height of the PCBs is 12 cm and the length is 18 cm. The clearance between the tips of the components on the PCB and the back surface of the adjacent PCB is 0.3 cm. The cooling air is supplied by a 15-W fan mounted at the inlet. If the temperature rise of air as it flows through the case of the computer is not to exceed 15°C, determine (a) the flow rate of the air that the fan needs to deliver, (b) the fraction of the temperature rise of air due to the heat generated by the fan and its motor, and (c) the highest allowable inlet air temperature if the surface temperature of the components is not to exceed 90°C anywhere in the system.
Get solution
15–111 An array of power transistors, each dissipating 2 W of power, is to be cooled by mounting them on a 20-cm x 20-cm square aluminum plate and blowing air over the plate with a fan at 30°C with a velocity of 3 m/s. The average temperature of the plate is not to exceed 60°C. Assuming the heat transfer from the back side of the plate to be negligible, determine the number of transistors that can be placed on this plate.
Get solution
15–112 Repeat Problem 15–111 for a location at an elevation of 1610 m where the atmospheric pressure is 83.4 kPa
Get solution
15–113 Reconsider Problem 15–111. Using EES (or other) software, investigate the effects of air velocity and the maximum plate temperature on the number of transistors. Let the air velocity vary from 1 rn/s to 8 m/s and the maximum plate temperature from 40ºC to 80ºC. Plot the number of transistors as functions of air velocity and maximum plate temperature, and discuss the results
Get solution
15–114 An enclosure contains an array of circuit boards, 15 cm high and 20 cm long. The clearance between the tips of the components on the PCB and the back surface of the adjacent PCB is 0.3 cm. Each circuit board contains 75 square chips on one side, each dissipating 0.15 W of power. Air enters the space between the boards through the 0.3-cm 15–cm cross section at 40°C with a velocity of 300 m/min. Assuming the heat transfer from the back side of the circuit board to be negligible, determine the exit temperature of the air and the highest surface temperature of the chips
Get solution
15–115 The components of an electronic system dissipating 120 W are located in a 1-m-long horizontal duct whose cross section is 20 cm 20 cm. The components in the duct are cooled by forced air, which enters at 30°C at a rate of 0.5 m3/min. Assuming 80 percent of the heat generated inside is transferred to air flowing through the duct and the remaining 20 percent is lost through the outer surfaces of the duct, determine (a) the exit temperature of air and (b) the highest component surface temperature in the duct
Get solution
15–116 Repeat Problem 15–115 for a circular horizontal duct of diameter 10 cm.
Get solution
15–117C If an electronic system can be cooled adequately by either forced-air cooling or liquid cooling, which one would you prefer? Why
Get solution
15–118C Explain how direct and indirect liquid cooling systems differ from each other
Get solution
15–119C Explain how closed-loop and open-loop liquid cooling systems operate
Get solution
15–120C What are the properties of a liquid ideally suited for cooling electronic equipment
Get solution
15–121 Acold plate that supports 10 power transistors, each dissipating 40 W, is to be cooled with water. It is specified that the temperature rise of the water not exceed 4°C and the velocity of water remain under 0.5 m/s. Assuming 25 percent of the heat generated is dissipated from the components to the surroundings by convection and radiation, and the remaining 75 percent is removed by the cooling water, determine the mass flow rate of water needed and the diameter of the pipe to satisfy the restriction imposed on the flow velocity. Also, determine the case temperature of the devices if the total case-to-liquid thermal resistance is 0.04°C/W and the water enters the cold plate at 25°C
Get solution
15–122 Reconsider Problem 15–121. Using EES (or other) software, investigate the effect of the maximum temperature rise of the water on the mass flow rate of water, the diameter of the pipe, and the case temperature. Let the maximum temperature rise vary from 1ºC to 10ºC. Plot the mass flow rate, the diameter, and the case temperature as a function of the temperature rise, and discuss the results
Get solution
15–123E Water enters the tubes of a cold plate at 95°F with an average velocity of 60 ft/min and leaves at 105°F. The diameter of the tubes is 0.25 in. Assuming 15 percent of the heat generated is dissipated from the components to the surroundings by convection and radiation, and the remaining 85 percent is removed by the cooling water, determine the amount of heat generated by the electronic devices mounted on the cold plate.
Get solution
15–124 Asealed electronic box is to be cooled by tap water flowing through channels on two of its sides. It is specified that the temperature rise of the water not exceed 3°C. The power dissipation of the box is 2 kW, which is removed entirely by water. If the box operates 24 h a day, 365 days a year, determine the mass flow rate of water flowing through the box and the amount of cooling water used per year
Get solution
15–125 Repeat Problem 15–124 for a power dissipation of 3 kW.
Get solution
15–126C What are the desirable characteristics of a liquid used in immersion cooling of electronic devices
Get solution
15–127C How does an open-loop immersion cooling system operate? How does it differ from closed-loop cooling systems
Get solution
15–128C How do immersion cooling systems with internal and external cooling differ? Why are externally cooled systems limited to relatively low-power applications
Get solution
15–129C Why is boiling heat transfer used in the cooling of very high-power electronic devices instead of forced air or liquid cooling
Get solution
15–130 A logic chip used in a computer dissipates 4 W of power and has a heat transfer surface area of 0.3 cm2. If the surface of the chip is to be maintained at 70°C while being cooled by immersion in a dielectric fluid at 20°C, determine the necessary heat transfer coefficient and the type of cooling mechanism that needs to be used to achieve that heat transfer coefficient
Get solution
15–131 A 6-W chip having a surface area of 0.5 cm2 is cooled by immersing it into FC86 liquid that is maintained at a temperature of 25°C. Using the boiling curve in Figure 15–63, estimate the temperature of the chip surface.
Get solution
15–132 A logic chip cooled by immersing it in a dielectric liquid dissipates 3.5 Wof power in an environment at 50°C and has a heat transfer surface area of 0.8 cm2. The surface temperature of the chip is measured to be 95°C. Assuming the heat transfer from the surface to be uniform, determine (a) the heat flux on the surface of the chip, in W/cm2; (b) the heat transfer coefficient on the surface of the chip, in W/m2 · °C; and (c) the thermal resistance between the surface of the chip and the cooling medium, in °C/W.
Get solution
15–133 Reconsider Problem 15–132. Using EES (or other) software, investigate the effect of chip power on the heat flux, the heat transfer coefficient, and the convection resistance on chip surface. Let the power vary from 2 W to 10 W. Plot the heat flux, the heat transfer coefficient, and the thermal resistance as a function of power dissipated, and discuss the results
Get solution
15–134 A computer chip dissipates 5 W of power and has a heat transfer surface area of 0.4 cm2. If the surface of the chip is to be maintained at 55°C while being cooled by immersion in a dielectric fluid at 10°C, determine the necessary heat transfer coefficient and the type of cooling mechanism that needs to be used to achieve that heat transfer coefficient
Get solution
15–135 A 3-W chip having a surface area of 0.2 cm2 is cooled by immersing it into FC86 liquid that is maintained at a temperature of 45°C. Using the boiling curve in Figure 15–63, estimate the temperature of the chip surface.
Get solution
15–136 Alogic chip having a surface area of 0.3 cm2 is to be cooled by immersing it into FC86 liquid that is maintained at a temperature of 35°C. The surface temperature of the chip is not to exceed 60°C. Using the boiling curve in Figure 15–63, estimate the maximum power that the chip can dissipate safely
Get solution
15–137 A 2-kW electronic device that has a surface area of 120 cm2 is to be cooled by immersing it in a dielectric fluid with a boiling temperature of 60°C contained in a 1-m x 1-m x 1-m cubic enclosure. Noting that the combined natural convection and the radiation heat transfer coefficients in air are typically about 10 W/m2 · °C, determine if the heat generated inside can be dissipated to the ambient air at 20°C by natural convection and radiation. If it cannot, explain what modification you could make to allow natural convection cooling. Also, determine the heat transfer coefficients at the surface of the electronic device for a surface temperature of 80°C. Assume the liquid temperature remains constant at 60°C throughout the enclosure.
Get solution
15–138C Several power transistors are to be cooled by mounting them on a water-cooled metal plate. The total power dissipation, the mass flow rate of water through the tube, and the water inlet temperature are fixed. Explain what you would do for the most effective cooling of the transistors
Get solution
15–139C Consider heat conduction along a vertical copper bar whose sides are insulated. One person claims that the bar should be oriented such that the hot end is at the bottom and the cold end is at the top for better heat transfer, since heat rises. Another person claims that it makes no differences to heat conduction whether heat is conducted downward or upward, and thus the orientation of the bar is irrelevant. With which person do you agree
Get solution
15–140 Consider a 15–cm 15–cm multilayer circuit board dissipating 22.5 W of heat. The board consists of four layers of 0.1-mm-thick copper (k 386 W/m · °C) and three layers of 0.5-mm-thick glass–epoxy (k 0.26 W/m · °C) sandwiched together, as shown in Figure P15–140. The circuit board is attached to a heat sink from both ends, and the temperature of the board at those ends is 35°C. Heat is considered to be uniformly generated in the epoxy layers of the PCB at a rate of 0.5 W per 1-cm x 15–cm epoxy laminate strip (or 1.5 W per 1-cm x 15–cm strip of the board). Considering only a portion of the PCB because of symmetry, determine the magnitude and location of the maximum temperature that occurs in the PCB. Assume heat transfer from the top and bottom faces of the PCB to be negligible.
Get solution
15–141 Repeat Problem 15–140, assuming that the board consists of a single 1.5-mm-thick layer of glass–epoxy, with no copper layers
Get solution
15–142 The components of an electronic system that is dissipating 150 W are located in a 1-m-long horizontal duct whose cross section is 10 cm 10 cm. The components in the duct are cooled by forced air, which enters at 30°C and 50 m/min and leaves at 45°C. The surfaces of the sheet metal duct are not painted, and so radiation heat transfer from the outer surfaces is negligible. If the ambient air temperature is 30°C, determine (a) the heat transfer from the outer surfaces of the duct to the ambient air by natural convection, (b) the average temperature of the duct, and (c) the highest component surface temperature in the duct
Get solution
15–143 Two 10-Wpower transistors are cooled by mounting them on the two sides of an aluminum bracket (k 237 W/m · °C) that is attached to a liquid-cooled plate by 0.2-mm-thick epoxy adhesive (k 1.8 W/m · °C), as shown in Figure P15–143. The thermal resistance of each plastic washer is given as 2°C/W, and the temperature of the cold plate is 40°C. The surface of the aluminum plate is untreated, and thus radiation heat transfer from it is negligible because of the low emissivity of aluminum surfaces. Disregarding heat transfer from the 0.3-cm-wide edges of the aluminum plate, determine the surface temperature of the transistor case. Also, determine the fraction of heat dissipation to the ambient air by natural convection and to the cold plate by conduction. Take the ambient temperature to be 25°C
Get solution
15–144E Afan blows air at 70°F and a velocity of 500 ft/min over a 1.5-Wplastic DIPwith 24 leads mounted on a PCB. Using data from Figure 15–23, determine the junction temperature of the electronic device. What would the junction temperature be if the fan were to fail
Get solution
15–145 A15–cm 18-cm double-sided circuit board dissipating a total of 18 W of heat is to be conduction-cooled by a 1.2-mm-thick aluminum core plate (k 237 W/m · °C) sandwiched between two epoxy laminates (k 0.26 W/m · °C). Each epoxy layer has a thickness of 0.5 mm and is attached to the aluminum core plate with conductive epoxy adhesive (k 1.8 W/m · °C) of thickness 0.1 mm. Heat is uniformly generated on each side of the PCB at a rate of 0.5 W per 1-cm x 15–cm epoxy laminate strip. All of the heat is conducted along the 18-cm side since the PCB is cooled along the two 15–cm-long edges. Considering only part of the PCB board because of symmetry, determine the maximum temperature rise across the 9-cm distance between the center and the sides of the PCB.
Get solution
15–146 Ten power transistors, each dissipating 2 W, are attached to a 7-cm x 7-cm x 0.2-cm aluminum plate with a square cutout in the middle in a symmetrical arrangement, as shown in Figure P15–146. The aluminum plate is cooled from two sides by liquid at 40°C. If 70 percent of the heat generated by the transistors is estimated to be conducted through the aluminum plate, determine the temperature rise across the 1-cmwide section of the aluminum plate between the transistors and the heat sink
Get solution
15–147 The components of an electronic system are located in a 1.2-m-long horizontal duct whose cross section is 10 cm x 20 cm. The components in the duct are not allowed to come into direct contact with cooling air, and so are cooled by air flowing over the duct at 30°C with a velocity of 250 m/min. The duct is oriented such that air strikes the 10-cm-high side of the duct normally. If the surface temperature of the duct is not to exceed 60°C, determine the total power rating of the electronic devices that can be mounted in the duct. What would your answer be if the duct is oriented such that air strikes the 20-cm-high side normally?
Get solution
15–148 Repeat Problem 15–147 for a location at an altitude of 5000 m, where the atmospheric pressure is 54.05 kPa
Get solution
15–149E Acomputer that consumes 65 Wof power is cooled by a fan blowing air into the computer enclosure. The dimensions of the computer case are 6 in. x 20 in. x 24 in., and all surfaces of the case are exposed to the ambient, except for the base surface. Temperature measurements indicate that the case is at an average temperature of 95°F when the ambient temperature and the temperature of the surrounding walls are 80°F. If the emissivity of the outer surface of the case is 0.85, determine the fraction of heat lost from the outer surfaces of the computer case.
Get solution
