Heat Transfer - Yunus Cengel - 2ed - Solutions: Heat Transfer - Yunus Cengel - 2ed

2–1C Is heat transfer a scalar or vector quantity? Explain. Answer the same question for temperature.
Get 2.1 exercise solution

2–2C How does transient heat transfer differ from steady heat transfer? How does one-dimensional heat transfer differ from two-dimensional heat transfer?
Get 2.2 exercise solution

2–3C Consider a cold canned drink left on a dinner table. Would you model the heat transfer to the drink as one-, two-, or three-dimensional? Would the heat transfer be steady or transient? Also, which coordinate system would you use to analyze this heat transfer problem, and where would you place the origin? Explain.
Get 2.3 exercise solution

2–4C Consider a round potato being baked in an oven. Would you model the heat transfer to the potato as one-, two-, or three-dimensional? Would the heat transfer be steady or transient? Also, which coordinate system would you use to solve this problem, and where would you place the origin? Explain.
Get 2.4 exercise solution

2–5C Consider an egg being cooked in boiling water in a pan. Would you model the heat transfer to the egg as one-, two-, or three-dimensional? Would the heat transfer be steady or transient? Also, which coordinate system would you use to solve this problem, and where would you place the origin? Explain.
Get 2.5 exercise solution

2–6C Consider a hot dog being cooked in boiling water in a pan. Would you model the heat transfer to the hot dog as one-, two-, or three-dimensional? Would the heat transfer be steady or transient? Also, which coordinate system would you use to solve this problem, and where would you place the origin? Explain.
Get 2.6 exercise solution

2–7C Consider the cooking process of a roast beef in an oven. Would you consider this to be a steady or transient heat transfer problem? Also, would you consider this to be one-, two-, or three-dimensional? Explain.
Get 2.7 exercise solution

2–8C Consider heat loss from a 200-L cylindrical hot water tank in a house to the surrounding medium. Would you consider this to be a steady or transient heat transfer problem? Also, would you consider this heat transfer problem to be one-, two-, or three-dimensional? Explain.
Get 2.8 exercise solution

2–9C Does a heat flux vector at a point P on an isothermal surface of a medium have to be perpendicular to the surface at that point? Explain.
Get 2.9 exercise solution

2–10C From a heat transfer point of view, what is the difference between isotropic and unisotropic materials?
Get 2.10 exercise solution

2–11C What is heat generation in a solid? Give examples.
Get 2.11 exercise solution

2–12C Heat generation is also referred to as energy generation or thermal energy generation. What do you think of these phrases?
Get 2.12 exercise solution

2–13C In order to determine the size of the heating element of a new oven, it is desired to determine the rate of heat transfer through the walls, door, and the top and bottom section of the oven. In your analysis, would you consider this to be a steady or transient heat transfer problem? Also, would you consider the heat transfer to be one-dimensional or multidimensional? Explain.
Get 2.13 exercise solution

2–14E The resistance wire of a 1000-W iron is 15 in. long and has a diameter of D = 0.08 in. Determine the rate of heat generation in the wire per unit volume, in Btu/h · ft3, and the heat flux on the outer surface of the wire, in Btu/h · ft2, as a result of this heat generation.
Get 2.14 exercise solution

2–15E Reconsider Problem 2–14E. Using EES (or other) software, evaluate and plot the surface heat flux as a function of wire diameter as the diameter varies from 0.02 to 0.20 in. Discuss the results.
Get 2.15 exercise solution

2–16 In a nuclear reactor, heat is generated uniformly in the 5-cm-diameter cylindrical uranium rods at a rate of 7 x 10e7 W/m3. If the length of the rods is 1 m, determine the rate of heat generation in each rod. Answer: 137.4 kW
Get 2.16 exercise solution

2–17 In a solar pond, the absorption of solar energy can be modeled as heat generation and can be approximated by g=g0e-bx, where g0 is the rate of heat absorption at the top surface per unit volume and b is a constant. Obtain a relation for the total rate of heat generation in a water layer of surface area A and thickness L at the top of the pond.
Get 2.17 exercise solution

2–18 Consider a large 3-cm-thick stainless steel plate in which heat is generated uniformly at a rate of 5 x 106 W/m3. Assuming the plate is losing heat from both sides, determine the heat flux on the surface of the plate during steady operation. Answer: 75,000 W/m2 Heat Conduction Equation
Get 2.18 exercise solution

2–19 Write down the one-dimensional transient heat conduction equation for a plane wall with constant thermal conductivity conductivity and heat generation in its simplest form, and indicate what each variable represents.
Get 2.19 exercise solution

2–20 Write down the one-dimensional transient heat conduction equation for a long cylinder with constant thermal conductivity and heat generation, and indicate what each variable represents.
Get 2.20 exercise solution

2–21 Starting with an energy balance on a rectangular volume element, derive the one-dimensional transient heat conduction equation for a plane wall with constant thermal conductivity and no heat generation.
Get 2.21 exercise solution

2–22 Starting with an energy balance on a cylindrical shell volume element, derive the steady one-dimensional heat conduction equation for a long cylinder with constant thermal conductivity in which heat is generated at a rate of g
Get 2.22 exercise solution

2–23 Starting with an energy balance on a spherical shell volume element, derive the one-dimensional transient heat conduction equation for a sphere with constant thermal conductivity and no heat generation.
Get 2.23 exercise solution

2–24 Consider a medium in which the heat conduction equation is given in its simplest form as

(a) Is heat transfer steady or transient? (b) Is heat transfer one-, two-, or three-dimensional? (c) Is there heat generation in the medium? (d) Is the thermal conductivity of the medium constant or variable?
Get 2.24 exercise solution

2–25 Consider a medium in which the heat conduction equation is given in its simplest form as

(a) Is heat transfer steady or transient? (b) Is heat transfer one-, two-, or three-dimensional? (c) Is there heat generation in the medium? (d) Is the thermal conductivity of the medium constant or variable?
Get 2.25 exercise solution

2–26 Consider a medium in which the heat conduction equation is given in its simplest form as

(a) Is heat transfer steady or transient? (b) Is heat transfer one-, two-, or three-dimensional? (c) Is there heat generation in the medium? (d) Is the thermal conductivity of the medium constant or variable?
Get 2.26 exercise solution

2–27 Consider a medium in which the heat conduction equation is given in its simplest form as

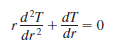
(a) Is heat transfer steady or transient? (b) Is heat transfer one-, two-, or three-dimensional? (c) Is there heat generation in the medium? (d) Is the thermal conductivity of the medium constant or variable?
Get 2.27 exercise solution

2–28 Starting with an energy balance on a volume element, derive the two-dimensional transient heat conduction equation in rectangular coordinates for T(x, y, t) for the case of constant thermal conductivity and no heat generation.
Get 2.28 exercise solution

2–29 Starting with an energy balance on a ring-shaped volume element, derive the two-dimensional steady heat conduction equation in cylindrical coordinates for T(r, z) for the case of constant thermal conductivity and no heat generation.
Get 2.29 exercise solution

2–30 Starting with an energy balance on a disk volume element, derive the one-dimensional transient heat conduction equation for T(z, t) in a cylinder of diameter D with an insulated side surface for the case of constant thermal conductivity with heat generation.
Get 2.30 exercise solution

2–31 Consider a medium in which the heat conduction equation is given in its simplest form as

(a) Is heat transfer steady or transient? (b) Is heat transfer one-, two-, or three-dimensional? (c) Is there heat generation in the medium? (d) Is the thermal conductivity of the medium constant or variable?
Get 2.33 exercise solution

2–34C What is a boundary condition? How many boundary conditions do we need to specify for a two-dimensional heat transfer problem?
Get 2.34 exercise solution

2–35C What is an initial condition? How many initial conditions do we need to specify for a two-dimensional heat transfer problem?
Get 2.35 exercise solution

2–36C What is a thermal symmetry boundary condition? How is it expressed mathematically?
Get 2.36 exercise solution

2–37C How is the boundary condition on an insulated surface expressed mathematically?
Get 2.37 exercise solution

2–38C It is claimed that the temperature profile in a medium must be perpendicular to an insulated surface. Is this a valid claim? Explain.
Get 2.38 exercise solution

2–39C Why do we try to avoid the radiation boundary conditions in heat transfer analysis?
Get 2.39 exercise solution

2–40 Consider a spherical container of inner radius r1, outer radius r2, and thermal conductivity k. Express the boundary condition on the inner surface of the container for steady onedimensional conduction for the following cases: (a) specified temperature of 50°C, (b) specified heat flux of 30 W/m2 toward the center, (c) convection to a medium at T with a heat transfer coefficient of h.
Get 2.40 exercise solution

2–41 Heat is generated in a long wire of radius r0 at a constant rate of g· 0 per unit volume. The wire is covered with a plastic insulation layer. Express the heat flux boundary condition at the interface in terms of the heat generated.
Get 2.41 exercise solution

2–42 Consider a long pipe of inner radius r1, outer radius r2, and thermal conductivity k. The outer surface of the pipe is subjected to convection to a medium at T with a heat transfer coefficient of h, but the direction of heat transfer is not known. Express the convection boundary condition on the outer surface of the pipe.
Get 2.42 exercise solution

2–43 Consider a spherical shell of inner radius r1, outer radius r2, thermal conductivity k, and emissivity E. The outer surface of the shell is subjected to radiation to surrounding surfaces at Tsurr, but the direction of heat transfer is not known. Express the radiation boundary condition on the outer surface of the shell.
Get 2.43 exercise solution

2–44 A container consists of two spherical layers, A and B, that are in perfect contact. If the radius of the interface is r0, express the boundary conditions at the interface.
Get 2.44 exercise solution

2–45 Consider a steel pan used to boil water on top of an electric range. The bottom section of the pan is L = 0.5 cm thick and has a diameter of D = 20 cm. The electric heating unit on the range top consumes 1000 Wof power during cooking, and 85 percent of the heat generated in the heating element is transferred uniformly to the pan. Heat transfer from the top surface of the bottom section to the water is by convection with a heat transfer coefficient of h. Assuming constant thermal conductivity and one-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary conditions) of this heat conduction problem during steady operation. Do not solve.
Get 2.45 exercise solution

2–46E A 2-kW resistance heater wire whose thermal conductivity is k = 10.4 Btu/h · ft · °F has a radius of r0 = 0.06 in. and a length of L = 15 in., and is used for space heating. Assuming constant thermal conductivity and one-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary conditions) of this heat conduction problem during steady operation. Do not solve.
Get 2.46 exercise solution

2–47 Consider an aluminum pan used to cook stew on top of an electric range. The bottom section of the pan is L = 0.25 cm thick and has a diameter of D = 18 cm. The electric heating unit on the range top consumes 900 W of power during cooking, and 90 percent of the heat generated in the heating element is transferred to the pan. During steady operation, the temperature of the inner surface of the pan is measured to be 108°C. Assuming temperature-dependent thermal conductivity and one-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary conditions) of this heat conduction problem during steady operation. Do not solve.
Get 2.47 exercise solution

2–48 Water flows through a pipe at an average temperature of T= 50°C. The inner and outer radii of the pipe are r1 = 6 cm and r2 = 6.5 cm, respectively. The outer surface of the pipe is wrapped with a thin electric heater that consumes 300 W per m length of the pipe. The exposed surface of the heater is heavily insulated so that the entire heat generated in the heater is transferred to the pipe. Heat is transferred from the inner surface of the pipe to the water by convection with a heat transfer coefficient of h = 55 W/m2 · °C. Assuming constant thermal conductivity and one-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary conditions) of the heat conduction in the pipe during steady operation. Do not solve.
Get 2.48 exercise solution

2–49 A spherical metal ball of radius r0 is heated in an oven to a temperature of Ti throughout and is then taken out of the oven and dropped into a large body of water at T where it is cooled by convection with an average convection heat transfer coefficient of h. Assuming constant thermal conductivity and transient one-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary and initial conditions) of this heat conduction problem. Do not solve.
Get 2.49 exercise solution

2–50 A spherical metal ball of radius r0 is heated in an oven to a temperature of Ti throughout and is then taken out of the oven and allowed to cool in ambient air at T by convection and radiation. The emissivity of the outer surface of the cylinder is E, and the temperature of the surrounding surfaces is Tsurr. The average convection heat transfer coefficient is estimated to be h. Assuming variable thermal conductivity and transient one-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary and initial conditions) of this heat conduction problem. Do not solve.
Get 2.50 exercise solution

2–51 Consider the north wall of a house of thickness L. The outer surface of the wall exchanges heat by both convection and radiation. The interior of the house is maintained at T 1, while the ambient air temperature outside remains at T 2. The sky, the ground, and the surfaces of the surrounding structures at this location can be modeled as a surface at an effective temperature of Tsky for radiation exchange on the outer surface. The radiation exchange between the inner surface of the wall and the surfaces of the walls, floor, and ceiling it faces is negligible. The convection heat transfer coefficients on the inner and outer surfaces of the wall are h1 and h2, respectively. The thermal conductivity of the wall material is k and the emissivity of the outer surface is E2. Assuming the heat transfer through the wall to be steady and one-dimensional, express the mathematical formulation (the differential equation and the boundary and initial conditions) of this heat conduction problem. Do not solve.
Get 2.51 exercise solution

2–52C Consider one-dimensional heat conduction through a large plane wall with no heat generation that is perfectly insulated on one side and is subjected to convection and radiation on the other side. It is claimed that under steady conditions, the temperature in a plane wall must be uniform (the same everywhere). Do you agree with this claim? Why?
Get 2.52 exercise solution

2–53C It is stated that the temperature in a plane wall with constant thermal conductivity and no heat generation varies linearly during steady one-dimensional heat conduction. Will this still be the case when the wall loses heat by radiation from its surfaces?
Get 2.53 exercise solution

2–54C Consider a solid cylindrical rod whose ends are maintained at constant but different temperatures while the side surface is perfectly insulated. There is no heat generation. It is claimed that the temperature along the axis of the rod varies linearly during steady heat conduction. Do you agree with this claim? Why?
Get 2.54 exercise solution

2–55C Consider a solid cylindrical rod whose side surface is maintained at a constant temperature while the end surfaces are perfectly insulated. The thermal conductivity of the rod material is constant and there is no heat generation. It is claimed that the temperature in the radial direction within the rod will not vary during steady heat conduction. Do you agree with this claim? Why?
Get 2.55 exercise solution

2–56 Consider a large plane wall of thickness L = 0.4 m, thermal conductivity k = 2.3 W/m · °C, and surface area A=20 m2. The left side of the wall is maintained at a constant temperature of T1 = 80°C while the right side loses heat by convection to the surrounding air at T= 15°C with a heat transfer coefficient of h = 24 W/m2 · °C. Assuming constant thermal conductivity and no heat generation in the wall, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the wall, (b) obtain a relation for the variation of temperature in the wall by solving the differential equation, and (c) evaluate the rate of heat transfer through the wall. Answer: (c) 6030 W
Get 2.56 exercise solution

2–57 Consider a solid cylindrical rod of length 0.15 m and diameter 0.05 m. The top and bottom surfaces of the rod are maintained at constant temperatures of 20°C and 95°C, respectively, while the side surface is perfectly insulated. Determine the rate of heat transfer through the rod if it is made of (a) copper, k = 380 W/m · °C, (b) steel, k = 18 W/m · °C, and (c) granite, k = 1.2 W/m · °C.
Get 2.57 exercise solution

2–58 Reconsider Problem 2–57. Using EES (or other) software, plot the rate of heat transfer as a function of the thermal conductivity of the rod in the range of 1 W/m · °C to 400 W/m · °C. Discuss the results.
Get 2.58 exercise solution

2–59 Consider the base plate of a 800-W household iron with a thickness of L = 0.6 cm, base area of A = 160 cm2, and thermal conductivity of k = 20 W/m · °C. The inner surface of the base plate is subjected to uniform heat flux generated by the resistance heaters inside. When steady operating conditions are reached, the outer surface temperature of the plate is measured to be 85°C. Disregarding any heat loss through the upper part of the iron, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the plate, (b) obtain a relation for the variation of temperature in the base plate by solving the differential equation, and (c) evaluate the inner surface temperature. Answer: (c) 100°C
Get 2.59 exercise solution

2–60 Repeat Problem 2–59 for a 1200-W iron.
Get 2.60 exercise solution

2–61 Reconsider Problem 2–59. Using the relation obtained for the variation of temperature in the base plate, plot the temperature as a function of the distance x in the range of x = 0 to x = L, and discuss the results. Use the EES (or other) software.
Get 2.61 exercise solution

2–62E Consider a steam pipe of length L = 15 ft, inner radius r1 = 2 in., outer radius r2 =2.4 in., and thermal conductivity k = 7.2 Btu/h · ft · °F. Steam is flowing through the pipe at an average temperature of 250°F, and the average convection heat transfer coefficient on the inner surface is given to be h =1.25 Btu/h · ft2 · °F . If the average temperature on the outer surfaces of the pipe is T2 160°F, (a) express the differential equation and the boundary conditions for steady onedimensional heat conduction through the pipe, (b) obtain a relation for the variation of temperature in the pipe by solving the differential equation, and (c) evaluate the rate of heat loss from the steam through the pipe. Answer: (c) 16,800 Btu/h
Get 2.62 exercise solution

2–63 Aspherical container of inner radius r1 = 2 m, outer radius r2 = 2.1 m, and thermal conductivity k =30 W/m · °C is filled with iced water at 0°C. The container is gaining heat by convection from the surrounding air at T= 25°C with a heat transfer coefficient of h = 18 W/m2 · °C. Assuming the inner surface temperature of the container to be 0°C, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the container, (b) obtain a relation for the variation of temperature in the container by solving the differential equation, and (c) evaluate the rate of heat gain to the iced water.
Get 2.63 exercise solution

2–64 Consider a large plane wall of thickness L = 0.3 m, thermal conductivity k = 2.5 W/m · °C, and surface area A =12 m2. The left side of the wall at x = 0 is subjected to a net heat flux of q·0 = 700 W/m2 while the temperature at that surface is measured to be T1 = 80°C. Assuming constant thermal conductivity and no heat generation in the wall, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the wall, (b) obtain a relation for the variation of temperature in the wall by solving the differential equation, and (c) evaluate the temperature of the right surface of the wall at x = L.
Get 2.64 exercise solution

2–65 Repeat Problem 2–64 for a heat flux of 950 W/m2 and a surface temperature of 85°C at the left surface at x = 0.
Get 2.65 exercise solution

2–66E A large steel plate having a thickness of L = 4 in., thermal conductivity of k = 7.2 Btu/h · ft · °F, and an emissivity of E= 0.6 is lying on the ground. The exposed surface of the plate at x = L is known to exchange heat by convection with the ambient air at T= 90°F with an average heat transfer coefficient of h = 12 Btu/h · ft2 · °F as well as by radiation with the open sky with an equivalent sky temperature of Tsky =510 R. Also, the temperature of the upper surface of the plate is measured to be 75°F. Assuming steady one-dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the plate, (b) obtain a relation for the variation of temperature in the plate by solving the differential equation, and (c) determine the value of the lower surface temperature of the plate at x = 0.
Get 2.66 exercise solution

2–67E Repeat Problem 2–66E by disregarding radiation heat transfer.
Get 2.67 exercise solution

2–68 When a long section of a compressed air line passes through the outdoors, it is observed that the moisture in the compressed air freezes in cold weather, disrupting and even completely blocking the air flow in the pipe. To avoid this problem, the outer surface of the pipe is wrapped with electric strip heaters and then insulated. Consider a compressed air pipe of length L = 6 m, inner radius r1 = 3.7 cm, outer radius r2 = 4.0 cm, and thermal conductivity k = 14 W/m · °C equipped with a 300-W strip heater. Air is flowing through the pipe at an average temperature of -10°C, and the average convection heat transfer coefficient on the inner surface is h = 30 W/m2 · °C. Assuming 15 percent of the heat generated in the strip heater is lost through the insulation, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the pipe, (b) obtain a relation for the variation of temperature in the pipe material by solving the differential equation, and (c) evaluate the inner and outer surface temperatures of the pipe.
Get 2.68 exercise solution

2–69 Reconsider Problem 2–68. Using the relation obtained for the variation of temperature in the pipe material, plot the temperature as a function of the radius r in the range of r = r1 to r = r2, and discuss the results. Use the EES (or other) software.
Get 2.69 exercise solution

2–70 In a food processing facility, a spherical container of inner radius r1 = 40 cm, outer radius r2 = 41 cm, and thermal conductivity k = 1.5 W/m · °C is used to store hot water and to keep it at 100°C at all times. To accomplish this, the outer surface of the container is wrapped with a 500-W electric strip heater and then insulated. The temperature of the inner surface of the container is observed to be nearly 100°C at all times. Assuming 10 percent of the heat generated in the heater is lost through the insulation, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the container, (b) obtain a relation for the variation of temperature in the container material by solving the differential equation, and (c) evaluate the outer surface temperature of the container. Also determine how much water at 100°C this tank can supply steadily if the cold water enters at 20°C.
Get 2.70 exercise solution

2–71 Reconsider Problem 2–70. Using the relation obtained for the variation of temperature in the container material, plot the temperature as a function of the radius r in the range of r = r1 to r = r2, and discuss the results. Use the EES (or other) software. Heat Generation in a Solid
Get 2.71 exercise solution

2–72C Does heat generation in a solid violate the first law of thermodynamics, which states that energy cannot be created or destroyed? Explain.
Get 2.72 exercise solution

2–73C What is heat generation? Give some examples.
Get 2.73 exercise solution

2–74C An iron is left unattended and its base temperature rises as a result of resistance heating inside. When will the rate of heat generation inside the iron be equal to the rate of heat loss from the iron?
Get 2.74 exercise solution

2–75C Consider the uniform heating of a plate in an environment at a constant temperature. Is it possible for part of the heat generated in the left half of the plate to leave the plate through the right surface? Explain.
Get 2.75 exercise solution

2–76C Consider uniform heat generation in a cylinder and a sphere of equal radius made of the same material in the same environment. Which geometry will have a higher temperature at its center? Why?
Get 2.76 exercise solution

2–77 A 2-kW resistance heater wire with thermal conductivity of k = 20 W/m · °C, a diameter of D =5 mm, and a length of L = 0.7 m is used to boil water. If the outer surface temperature of the resistance wire is Ts = 110°C, determine the temperature at the center of the wire.
Get 2.77 exercise solution

2–78 Consider a long solid cylinder of radius r0 = 4 cm and thermal conductivity k = 25 W/m · °C. Heat is generated in the cylinder uniformly at a rate of g0 = 35 W/cm3. The side surface of the cylinder is maintained at a constant temperature of Ts = 80°C. The variation of temperature in the cylinder is given by

Based on this relation, determine (a) if the heat conduction is steady or transient, (b) if it is one-, two-, or three-dimensional, and (c) the value of heat flux on the side surface of the cylinder at r = r0.
Get 2.78 exercise solution

2–79 Reconsider Problem 2–78. Using the relation obtained for the variation of temperature in the cylinder, plot the temperature as a function of the radius r in the range of r = 0 to r = r0, and discuss the results. Use the EES (or other) software.
Get 2.79 exercise solution

2–80E A long homogeneous resistance wire of radius r0 = 0.25 in. and thermal conductivity k = 8.6 Btu/h · ft · °F is being used to boil water at atmospheric pressure by the passage of electric current. Heat is generated in the wire uniformly as a result of resistance heating at a rate of g= 1800 Btu/h · in3. The heat generated is transferred to water at 212°F by convection with an average heat transfer coefficient of h = 820 Btu/h · ft2 · °F. Assuming steady one-dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the wire, (b) obtain a relation for the variation of temperature in the wire by solving the differential equation, and (c) determine the temperature at the centerline of the wire. Answer: (c) 290.8°F
Get 2.80 exercise solution

2–81E Reconsider Problem 2–80E. Using the relation obtained for the variation of temperature in the wire, plot the temperature at the centerline of the wire as a function of the heat generation g · in the range of 400 Btu/h · in3 to 2400 Btu/h · in3, and discuss the results. Use the EES (or other) software.
Get 2.81 exercise solution

2–82 In a nuclear reactor, 1-cm-diameter cylindrical uranium rods cooled by water from outside serve as the fuel. Heat is generated uniformly in the rods (k = 29.5 W/m · °C) at a rate of 7 x 107 W/m3. If the outer surface temperature of rods is 175°C, determine the temperature at their center.
Get 2.82 exercise solution

2–83 Consider a large 3-cm-thick stainless steel plate (k = 15.1 W/m · °C) in which heat is generated uniformly at a rate of 5 x 105 W/m3. Both sides of the plate are exposed to an environment at 30°C with a heat transfer coefficient of 60 W/m2 · °C. Explain where in the plate the highest and the lowest temperatures will occur, and determine their values.
Get 2.83 exercise solution

2–84 Consider a large 5-cm-thick brass plate (k = 111 W/m · °C) in which heat is generated uniformly at a rate of 2 x 105 W/m3. One side of the plate is insulated while the other side is exposed to an environment at 25°C with a heat transfer coefficient of 44 W/m2 · °C. Explain where in the plate the highest and the lowest temperatures will occur, and determine their values.
Get 2.84 exercise solution

2–85 Reconsider Problem 2–84. Using EES (or other) software, investigate the effect of the heat transfer coefficient on the highest and lowest temperatures in the plate. Let the heat transfer coefficient vary from 20 W/m2 · °C to 100 W/m2 · °C. Plot the highest and lowest temperatures as a function of the heat transfer coefficient, and discuss the results.
Get 2.85 exercise solution

2–86 A 6-m-long 2-kW electrical resistance wire is made of 0.2-cm-diameter stainless steel (k = 15.1 W/m · °C). The resistance wire operates in an environment at 30°C with a heat transfer coefficient of 140 W/m2 · °C at the outer surface. Determine the surface temperature of the wire (a) by using the applicable relation and (b) by setting up the proper differential equation and solving it. Answers: (a) 409°C, (b) 409°C
Get 2.86 exercise solution

2–87E Heat is generated uniformly at a rate of 3 kW per ft length in a 0.08-in.-diameter electric resistance wire made of nickel steel (k = 5.8 Btu/h · ft · °F). Determine the temperature difference between the centerline and the surface of the wire.
Get 2.87 exercise solution

2–88E Repeat Problem 2–87E for a manganese wire (k = 4.5 Btu/h · ft · °F).
Get 2.88 exercise solution

2–89 Consider a homogeneous spherical piece of radioactive material of radius r0 = 0.04 m that is generating heat at a constant rate of g= 4 x 107 W/m3. The heat generated is dissipated to the environment steadily. The outer surface of the sphere is maintained at a uniform temperature of 80°C and the thermal conductivity of the sphere is k = 15 W/m · °C. Assuming steady one-dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the sphere, (b) obtain a relation for the variation of temperature in the sphere by solving the differential equation, and (c) determine the temperature at the center of the sphere.
Get 2.89 exercise solution

2–90 Reconsider Problem 2–89. Using the relation obtained for the variation of temperature in the sphere, plot the temperature as a function of the radius r in the range of r = 0 to r = r0. Also, plot the center temperature of the sphere as a function of the thermal conductivity in the range of 10 W/m · °C to 400 W/m · °C. Discuss the results. Use the EES (or other) software.
Get 2.90 exercise solution

2–91 A long homogeneous resistance wire of radius r0 = 5 mm is being used to heat the air in a room by the passage of electric current. Heat is generated in the wire uniformly at a rate of g= 5 x 107 W/m3 as a result of resistance heating. If the temperature of the outer surface of the wire remains at 180°C, determine the temperature at r = 2 mm after steady operation conditions are reached. Take the thermal conductivity of the wire to be k = 8 W/m · °C.
Get 2.91 exercise solution

2–92 Consider a large plane wall of thickness L = 0.05 m. The wall surface at x = 0 is insulated, while the surface at x = L is maintained at a temperature of 30°C. The thermal conductivity of the wall is k = 30 W/m · °C, and heat is generated in the wall at a rate of g= g0e-0.5x/L W/m3 where g0= 8 x 10 6 W/m3. Assuming steady one-dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the wall, (b) obtain a relation for the variation of temperature in the wall by solving the differential equation, and (c) determine the temperature of the insulated surface of the wall.
Get 2.92 exercise solution

2–93 Reconsider Problem 2–92. Using the relation given for the heat generation in the wall, plot the heat generation as a function of the distance x in the range of x = 0 to x = L, and discuss the results. Use the EES (or other) software. Variable Thermal Conductivity, k (T )
Get 2.93 exercise solution

2–94C Consider steady one-dimensional heat conduction in a plane wall, long cylinder, and sphere with constant thermal conductivity and no heat generation. Will the temperature in any of these mediums vary linearly? Explain.
Get 2.94 exercise solution

2–95C Is the thermal conductivity of a medium, in general, constant or does it vary with temperature?
Get 2.95 exercise solution

2–96C Consider steady one-dimensional heat conduction in a plane wall in which the thermal conductivity varies linearly. The error involved in heat transfer calculations by assuming constant thermal conductivity at the average temperature is (a) none, (b) small, or (c) significant.
Get 2.96 exercise solution

2–97C The temperature of a plane wall during steady onedimensional heat conduction varies linearly when the thermal conductivity is constant. Is this still the case when the thermal conductivity varies linearly with temperature?
Get 2.97 exercise solution

2–98C When the thermal conductivity of a medium varies linearly with temperature, is the average thermal conductivity always equivalent to the conductivity value at the average temperature?
Get 2.98 exercise solution

2–99 Consider a plane wall of thickness L whose thermal conductivity varies in a specified temperature range as k(T) = k0(1 + BT2) where k0 and B are two specified constants. The wall surface at x = 0 is maintained at a constant temperature of T1, while the surface at x = L is maintained at T2. Assuming steady one-dimensional heat transfer, obtain a relation for the heat transfer rate through the wall.
Get 2.99 exercise solution

2–100 Consider a cylindrical shell of length L, inner radius r1, and outer radius r2 whose thermal conductivity varies linearly in a specified temperature range as k(T) = k0(1 + BT) where k0 and B are two specified constants. The inner surface of the shell is maintained at a constant temperature of T1, while the outer surface is maintained at T2. Assuming steady onedimensional heat transfer, obtain a relation for (a) the heat transfer rate through the wall and (b) the temperature distribution T(r) in the shell.
Get 2.100 exercise solution

2–101 Consider a spherical shell of inner radius r1 and outer radius r2 whose thermal conductivity varies linearly in a specified temperature range as k(T) = k0(1 +BT) where k0 and B are two specified constants. The inner surface of the shell is maintained at a constant temperature of T1 while the outer surface is maintained at T2. Assuming steady one-dimensional heat transfer, obtain a relation for (a) the heat transfer rate through the shell and (b) the temperature distribution T(r) in the shell.
Get 2.101 exercise solution

2–102 Consider a 1.5-m-high and 0.6-m-wide plate whose thickness is 0.15 m. One side of the plate is maintained at a constant temperature of 500 K while the other side is maintained at 350 K. The thermal conductivity of the plate can be assumed to vary linearly in that temperature range as k(T) = k0(1 +BT) where k0 =25 W/m · K and B= 8.7 x 10-4 K-1. Disregarding the edge effects and assuming steady onedimensional heat transfer, determine the rate of heat conduction through the plate.
Get 2.102 exercise solution

2–103 Reconsider Problem 2–102. Using EES (or other) software, plot the rate of heat conduction through the plate as a function of the temperature of the hot side of the plate in the range of 400 K to 700 K. Discuss the results. Special Topic: Review of Differential Equations
Get 2.103 exercise solution

2–104C Why do we often utilize simplifying assumptions when we derive differential equations?
Get 2.104 exercise solution

2–105C What is a variable? How do you distinguish a dependent variable from an independent one in a problem?
Get 2.105 exercise solution

2–106C Can a differential equation involve more than one independent variable? Can it involve more than one dependent variable? Give examples.
Get 2.106 exercise solution

2–107C What is the geometrical interpretation of a derivative? What is the difference between partial derivatives and ordinary derivatives?
Get 2.107 exercise solution

2–108C What is the difference between the degree and the order of a derivative?
Get 2.108 exercise solution

2–109C Consider a function f(x, y) and its partial derivative df/dx. Under what conditions will this partial derivative be equal to the ordinary derivative df/dx?
Get 2.109 exercise solution

2–110C Consider a function f(x) and its derivative df/dx. Does this derivative have to be a function of x?
Get 2.110 exercise solution

2–111C How is integration related to derivation?
Get 2.111 exercise solution

2–112C What is the difference between an algebraic equation and a differential equation?
Get 2.112 exercise solution

2–113C What is the difference between an ordinary differential equation and a partial differential equation?
Get 2.113 exercise solution

2–114C How is the order of a differential equation determined?
Get 2.114 exercise solution

2–115C How do you distinguish a linear differential equation from a nonlinear one?
Get 2.115 exercise solution

2–116C How do you recognize a linear homogeneous differential equation? Give an example and explain why it is linear and homogeneous.
Get 2.116 exercise solution

2–117C How do differential equations with constant coefficients differ from those with variable coefficients? Give an example for each type.
Get 2.117 exercise solution

2–118C What kind of differential equations can be solved by direct integration?
Get 2.118 exercise solution

2–119C Consider a third order linear and homogeneous differential equation. How many arbitrary constants will its general solution involve? Review Problems
Get 2.119 exercise solution

2–120 Consider a small hot metal object of mass m and specific heat C that is initially at a temperature of Ti. Now the object is allowed to cool in an environment at T by convection with a heat transfer coefficient of h. The temperature of the metal object is observed to vary uniformly with time during cooling. Writing an energy balance on the entire metal object, derive the differential equation that describes the variation of temperature of the ball with time, T(t). Assume constant thermal conductivity and no heat generation in the object. Do not solve.
Get 2.120 exercise solution

2–121 Consider a long rectangular bar of length a in the x-direction and width b in the y-direction that is initially at a uniform temperature of Ti. The surfaces of the bar at x = 0 and y = 0 are insulated, while heat is lost from the other two surfaces by convection to the surrounding medium at temperature T with a heat transfer coefficient of h. Assuming constant thermal conductivity and transient two-dimensional heat transfer with no heat generation, express the mathematical formulation (the differential equation and the boundary and initial conditions) of this heat conduction problem. Do not solve.
Get 2.121 exercise solution

2–122 Consider a short cylinder of radius r0 and height H in which heat is generated at a constant rate of g· 0. Heat is lost from the cylindrical surface at r = r0 by convection to the surrounding medium at temperature T with a heat transfer coefficient of h. The bottom surface of the cylinder at z = 0 is insulated, while the top surface at z = H is subjected to uniform heat flux q· h. Assuming constant thermal conductivity and steady two-dimensional heat transfer, express the mathematical formulation (the differential equation and the boundary conditions) of this heat conduction problem. Do not solve.
Get 2.122 exercise solution

2–123E Consider a large plane wall of thickness L = 0.5 ft and thermal conductivity k = 1.2 Btu/h · ft · °F. The wall is covered with a material that has an emissivity of E= 0.80 and a solar absorptivity of a= 0.45. The inner surface of the wall is maintained at T1 = 520 R at all times, while the outer surface is exposed to solar radiation that is incident at a rate of qsolar = 300 Btu/h · ft2. The outer surface is also losing heat by radiation to deep space at 0 K. Determine the temperature of the outer surface of the wall and the rate of heat transfer through the wall when steady operating conditions are reached. Answers: 530.9 R, 26.2 Btu/h · ft2
Get 2.123 exercise solution

2–124E Repeat Problem 2–123E for the case of no solar radiation incident on the surface.
Get 2.124 exercise solution

2–125 Consider a steam pipe of length L, inner radius r1, outer radius r2, and constant thermal conductivity k. Steam flows inside the pipe at an average temperature of Ti with a convection heat transfer coefficient of hi. The outer surface of the pipe is exposed to convection to the surrounding air at a temperature of T0 with a heat transfer coefficient of ho. Assuming steady one-dimensional heat conduction through the pipe, (a) express the differential equation and the boundary conditions for heat conduction through the pipe material, (b) obtain a relation for the variation of temperature in the pipe material by solving the differential equation, and (c) obtain a relation for the temperature of the outer surface of the pipe.
Get 2.125 exercise solution

2–126 The boiling temperature of nitrogen at atmospheric pressure at sea level (1 atm pressure) is -196°C. Therefore, nitrogen is commonly used in low temperature scientific studies since the temperature of liquid nitrogen in a tank open to the atmosphere will remain constant at -196°C until the liquid nitrogen in the tank is depleted. Any heat transfer to the tank will result in the evaporation of some liquid nitrogen, which has a heat of vaporization of 198 kJ/kg and a density of 810 kg/m3 at 1 atm. Consider a thick-walled spherical tank of inner radius r1 =2 m, outer radius r2 2.1 m , and constant thermal conductivity k = 18 W/m · °C. The tank is initially filled with liquid nitrogen at 1 atm and -196°C, and is exposed to ambient air at T = 20°C with a heat transfer coefficient of h =25 W/m2 · °C. The inner surface temperature of the spherical tank is observed to be almost the same as the temperature of the nitrogen inside. Assuming steady one-dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the tank, (b) obtain a relation for the variation of temperature in the tank material by solving the differential equation, and (c) determine the rate of evaporation of the liquid nitrogen in the tank as a result of the heat transfer from the ambient air.
Get 2.126 exercise solution

2–127 Repeat Problem 2–126 for liquid oxygen, which has a boiling temperature of -183°C, a heat of vaporization of 213 kJ/kg, and a density of 1140 kg/m3 at 1 atm.
Get 2.127 exercise solution

2–128 Consider a large plane wall of thickness L = 0.4 m and thermal conductivity k = 8.4 W/m · °C. There is no access to the inner side of the wall at x = 0 and thus the thermal conditions on that surface are not known. However, the outer surface of the wall at x = L, whose emissivity is E=0.7, is known to exchange heat by convection with ambient air at T = 25°C with an average heat transfer coefficient of h = 14 W/m2 · °C as well as by radiation with the surrounding surfaces at an average temperature of Tsurr = 290 K. Further, the temperature of the outer surface is measured to be T2 = 45°C. Assuming steady one-dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the plate, (b) obtain a relation for the temperature of the outer surface of the plate by solving the differential equation, and (c) evaluate the inner surface temperature of the wall at x = 0.
Get 2.128 exercise solution

2–129 A 1000-W iron is left on the iron board with its base exposed to ambient air at 20°C. The base plate of the iron has a thickness of L = 0.5 cm, base area of A = 150 cm2, and thermal conductivity of k = 18 W/m · °C. The inner surface of the base plate is subjected to uniform heat flux generated by the resistance heaters inside. The outer surface of the base plate whose emissivity is E= 0.7, loses heat by convection to ambient air at T = 22° C with an average heat transfer coefficient of h = 30 W/m2 · °C as well as by radiation to the surrounding surfaces at an average temperature of Tsurr = 290 K. Disregarding any heat loss through the upper part of the iron, (a) express the differential equation and the boundary conditions for steady one-dimensional heat conduction through the plate, (b) obtain a relation for the temperature of the outer surface of the plate by solving the differential equation, and (c) evaluate the outer surface temperature.
Get 2.129 exercise solution

2–130 Repeat Problem 2–129 for a 1500-W iron.
Get 2.130 exercise solution

2–131E The roof of a house consists of a 0.8-ft-thick concrete slab (k = 1.1 Btu/h · ft · °F) that is 25 ft wide and 35 ft long. The emissivity of the outer surface of the roof is 0.8, and the convection heat transfer coefficient on that surface is estimated to be 3.2 Btu/h · ft2 · °F. On a clear winter night, the ambient air is reported to be at 50°F, while the night sky temperature for radiation heat transfer is 310 R. If the inner surface temperature of the roof is T1 = 62°F, determine the outer surface temperature of the roof and the rate of heat loss through the roof when steady operating conditions are reached.
Get 2.131 exercise solution

2–132 Consider a long resistance wire of radius r1 = 0.3 cm and thermal conductivity kwire = 18 W/m · °C in which heat is generated uniformly at a constant rate of g· = 1.5 W/cm3 as a result of resistance heating. The wire is embedded in a 0.4-cmthick layer of plastic whose thermal conductivity is kplastic = 1.8 W/m · °C. The outer surface of the plastic cover loses heat by convection to the ambient air at T = 25°C with an average combined heat transfer coefficient of h = 14 W/m2 · °C. Assuming one-dimensional heat transfer, determine the temperatures at the center of the resistance wire and the wire-plastic layer interface under steady conditions.
Get 2.132 exercise solution

2–133 Consider a cylindrical shell of length L, inner radius r1, and outer radius r2 whose thermal conductivity varies in a specified temperature range as k(T) = k0(1 +BT 2) where k0 and B are two specified constants. The inner surface of the shell is maintained at a constant temperature of T1 while the outer surface is maintained at T2. Assuming steady onedimensional heat transfer, obtain a relation for the heat transfer rate through the shell.
Get 2.133 exercise solution

2–134 In a nuclear reactor, heat is generated in 1-cmdiameter cylindrical uranium fuel rods at a rate of 4 x 107 W/m3. Determine the temperature difference between the center and the surface of the fuel rod.
Get 2.134 exercise solution

2–135 Consider a 20-cm-thick large concrete plane wall (k = 0.77 W/m · °C) subjected to convection on both sides with T1 = 27°C and h1 = 5 W/m2 · °C on the inside, and T 2 = 8°C and h2 = 12 W/m2 · °C on the outside. Assuming constant thermal conductivity with no heat generation and negligible radiation, (a) express the differential equations and the boundary conditions for steady one-dimensional heat conduction through the wall, (b) obtain a relation for the variation of temperature in the wall by solving the differential equation, and (c) evaluate the temperatures at the inner and outer surfaces of the wall.
Get 2.135 exercise solution

2–136 Consider a water pipe of length L = 12 m, inner radius r1 = 15 cm, outer radius r2 = 20 cm, and thermal conductivity k =20 W/m · °C. Heat is generated in the pipe material uniformly by a 25-kW electric resistance heater. The inner and outer surfaces of the pipe are at T1 = 60°C and T2 = 80°C, respectively. Obtain a general relation for temperature distribution inside the pipe under steady conditions and determine the temperature at the center plane of the pipe.
Get 2.136 exercise solution

2–137 Heat is generated uniformly at a rate of 2.6 x 106 W/m3 in a spherical ball (k = 45 W/m · °C) of diameter 30 cm. The ball is exposed to iced-water at 0°C with a heat transfer coefficient of 1200 W/m2 · °C. Determine the temperatures at the center and the surface of the ball.
Get 2.137 exercise solution

Heat Transfer - Yunus Cengel - 2ed - Chapter 2- Solutions